VENTS ET COURANTS-JETS

VENTS ET COURANTS-JETS

Sous l’influence des inégalités d’absorption de l’énergie provenant du rayonnement solaire, inégalités qui résultent essentiellement de la forme sphérique de la Terre, de la répartition des océans et des continents ainsi que de la couverture nuageuse de notre planète, apparaissent à la surface du globe et dans l’atmosphère des différences de température qui modèlent le champ de pression et engendrent les courants aériens qui agitent perpétuellement l’air atmosphérique.

C’est la vitesse de déplacement de l’air en chaque point qui définit le vent. On peut donc le représenter comme un vecteur Vdéfini par ses trois composantes (u , v, w ) sur les trois axes d’un trièdre de référence. Celui-ci est souvent constitué par deux axes choisis dans un plan horizontal tangent à la surface du globe, à savoir un axe dirigé selon la tangente au parallèle de latitude et orienté vers l’est, et un axe tangent au méridien de longitude et orienté vers le pôle, le troisième axe étant la verticale du lieu orientée vers le haut. Dans un tel trièdre, les trois composantes du vent sont respectivement: sa composante zonale (u ), sa composante méridienne (v) et sa composante verticale (w ).

La pression atmosphérique diminue rapidement avec l’altitude (surtout dans les couches inférieures de l’atmosphère), si bien qu’au-dessus du niveau de 60 kilomètres, niveau pris généralement comme limite pour l’atmosphère des météorologistes, il ne reste plus guère qu’un millième de la masse totale atmosphérique. Le rayon de la Terre étant de l’ordre de 6 000 kilomètres, une épaisseur de 60 kilomètres est donc de l’ordre du centième du rayon terrestre. Si l’on observe l’écoulement de l’air sans entrer dans le détail, comme pourrait le faire un astronaute à partir d’une station orbitale, on conçoit qu’à grande échelle les mouvements généraux de l’air soient essentiellement horizontaux.

À cette échelle, la composante verticale (w ) du vecteur vent Vest négligeable devant sa composante horizontale bien qu’elle joue par ailleurs un rôle essentiel, notamment pour la formation des précipitations, mais dans des zones d’extension limitée.

L’un des aspects le plus remarquables de la circulation quasi horizontale est présenté par les courants-jets, sortes de tubes aplatis de vent fort, que l’on observe au-dessus de certaines régions du globe. L’épaisseur des courants-jets est de l’ordre de 3 à 5 kilomètres, leur largeur de 500 à 800 kilomètres, et leur longueur en atteint plusieurs milliers. Leur axe, où le vent est maximal, se situe sous la tropopause, à une altitude qui est fréquemment voisine de 9 à 11 kilomètres dans les régions tempérées, plus élevée (de 11 à 14 km) dans les régions subtropicales et plus basse dans les régions de haute latitude. Les vitesses maximales atteignent fréquemment 300 et même, occasionnellement, 400 kilomètres par heure. L’appellation de courant-jet (jet-stream ), donnée par les météorologistes américains, est quelque peu fallacieuse dans la mesure où la notion de courant suggère (par analogie avec les courants marins, par exemple) la permanence du phénomène. Or le courant-jet n’a ni la continuité ni la permanence du Gulf Stream et, s’il est rarement absent sur une carte hémisphérique de vents en altitude, sa position est extrêmement fluctuante d’un jour à l’autre, de même que son intensité et, dans une moindre mesure, son altitude.

1. Direction du vent

Puisque le vent (synoptique) est considéré comme horizontal, on peut repérer la direction du vent dans le plan de l’horizon. On utilise souvent comme système de repérage un ensemble de directions divisant en angles égaux les quadrants déterminés par les quatre points cardinaux: c’est ce que l’on appelle la rose des vents. Par convention, la direction du vent est toujours celle «d’où vient» le vent: ainsi un vent d’ouest est un vent qui souffle de l’ouest vers l’est. La direction du vent, déterminée à l’aide d’une girouette, est exprimée:

– soit en «rose de 32» directions; est (E) = 08, sud (S) = 16, ouest (W) = 24, nord (N) = 32;

– soit en «rose de 36» directions; est (E) = 09, sud (S) = 18, ouest (W) = 27, nord (N) = 36.

L’indication 00 correspond à un «vent calme» (pas de direction déterminée).

2. Mesure du vent en surface

La vitesse du vent en surface est mesurée à l’aide d’un anémomètre, formé d’un moulinet tournant autour d’un axe vertical et actionnant un petit générateur électrique, l’intensité du courant étant fonction de sa vitesse de rotation, donc de la vitesse du vent. Les anémogirouettes, constituées d’un moulinet anémométrique à axe horizontal orienté face au vent par une girouette, sont pratiquement abandonnées. Des anémomètres électroniques à fil chaud (refroidi par le vent) sont utilisés pour les faibles vitesses (jusqu’à 4 m/s environ). À défaut d’anémomètre, on peut estimer la vitesse du vent d’après l’échelle de Beaufort (cf. tableau).

Les satellites météorologiques permettent d’estimer la vitesse et la direction du vent à partir de l’étude du déplacement des nuages; cette mesure est cependant imprécise du fait de l’incertitude sur l’altitude. En revanche, les diffusiomètres-radars embarqués à bord de certains satellites en orbite basse (comme Seasat, en 1978, ou les E.R.S., dont le deuxième exemplaire a été lancé le 21 avril 1995) conduisent à la connaissance de la vitesse et de la direction du vent à la surface des océans. À titre d’exemple, E.R.S.-1 fournit un million de points de mesure toutes les 72 heures (la gamme des vitesses est comprise entre 0,5 et 25 m/s, avec une précision de 2 m/s ou de 10 p. 100, et de 梁 20⁰ en direction, sur une grille dont le maillage est de 25 km).

Dans les messages météorologique échangés sur les circuits internationaux, les données relatives à la vitesse et à la direction du vent résultent d’une moyenne effectuée sur les dix minutes précédant l’heure de l’observation. Cette règle est destinée à n’échanger que des données relatives au vent synoptique, seules significatives pour évaluer l’évolution des grands courants aériens.

Lorsqu’il s’agit d’une observation destinée à une utilisation à brève échéance (pour l’atterrissage d’un avion par exemple), la direction et la vitesse du vent résultent d’une moyenne sur une durée plus courte (deux minutes pour le vent aéronautique).

La détermination du vent instantané, soumis aux influences des obstacles locaux, n’offre pas d’intérêt en général sauf dans le cas de l’estimation de rafales destructrices. À cette échelle, le vent ne peut plus être considéré comme horizontal et sa description complète nécessite la mesure de ses trois composantes.

3. Mesure du vent en altitude

La mesure du vent en altitude s’effectue par la poursuite d’un ballon à l’aide de la lunette d’un théodolite permettant de déterminer, à chaque instant, l’azimut et l’inclinaison de la direction du ballon. Ces indications combinées avec l’altitude du ballon (dont la vitesse ascensionnelle supposée constante a été fixée au départ par un tarage) facilitent la détermination des positions successives du ballon et, par suite, le calcul de la direction et de la vitesse du vent tout au long de la trajectoire. Ce procédé de poursuite optique est évidemment limité par la présence de nuages; aussi disparaît-il au bénéfice de procédés de poursuite radioélectrique: radiothéodolites, radars, utilisation des chaînes de radiolocalisation. Dans ces cas, on s’affranchit de l’hypothèse sur la vitesse ascensionnelle du ballon en dotant ce dernier d’un baromètre couplé avec un petit émetteur radio permettant de recevoir ses indications à la station de lancement.

4. Le vent et le champ de pression atmosphérique

À grande échelle, l’accélération du vent synoptique est très faible. Il en résulte qu’on peut considérer, avec une bonne approximation, que les forces qui s’exercent sur une particule d’air, isolée par la pensée du milieu extérieur et de masse m prise égale à l’unité, sont en équilibre.

Forces en jeu

Abstraction faite des forces de frottement qui sont négligeables en atmosphère libre, c’est-à-dire au-dessus de la couche dont l’écoulement est perturbé par la rugosité du sol et dont l’épaisseur ne dépasse pas quelques hectomètres, ces forces sont au nombre de trois: la pesanteur, la force de pression et la force de Coriolis.

La pesanteur て (poids de la particule d’air) est verticale et dirigée vers le bas. On a て = m む , où む est l’accélération de la pesanteur, soit, pour une particule d’air de masse unité, て = む.

La force de pression は est normale aux surfaces isobares et dirigée des hautes pressions vers les basses pressions. Cette force représente la résultante des contraintes que le milieu extérieur à la particule exerce sur elle. Comme les surfaces isobares sont quasi horizontales (leur pente est inférieure à 1/2 000), la force de pression est quasi verticale; cependant, en dépit de la faible inclinaison des surfaces isobares, la force du vent en un point est directement proportionnelle à la pente de la surface isobare qui passe en ce point. Pour une particule d’air de masse unité, cette force a pour valeur:

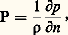où 煉p / 煉n représente le taux de variation de la pression selon la normale à la surface isobare orientée vers le haut, et 福 la masse volumique de la particule d’air.

La force de Coriolis ぢ est une force déviante due à la rotation de la Terre autour de l’axe des pôles. Tout objet mobile par rapport à la surface du globe est soumis à une force d’entraînement; cela traduit simplement le fait que la participation du mobile à la rotation terrestre intervient dans toute variation de sa vitesse, c’est-à-dire dans son accélération. Cette force est perpendiculaire au plan formé par l’axe des pôles et par le vecteur vitesse du mobile. Elle est donc perpendiculaire ici à la vitesse du vent et, de plus, elle est dirigée sur la droite du vent dans l’hémisphère Nord, sur sa gauche dans l’hémisphère Sud. L’expression de cette force pour une particule d’air de masse unité est:

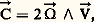où est le vecteur rotation de la Terre (dirigé selon l’axe des pôles et proportionnel à la vitesse de rotation de la Terre sur elle-même, soit 2 神/86 164, exprimée en radians par seconde) et ふ la vitesse du vent.

Dans les problèmes habituels de la mécanique (mouvement d’une automobile par exemple), cette force déviante est parfaitement négligeable, mais elle intervient sur la trajectoire d’un projectile à grande vitesse (obus, fusée, satellite); elle intervient également, et de façon déterminante en dépit de son extrême petitesse, dans les déplacements atmosphériques en raison de la faiblesse des forces qui contribuent à mettre l’air en mouvement.

Soit un point O de l’atmosphère et p la portion de surface isobare assimilable à un plan en ce point (fig. 1).

Soit Otla ligne de plus grande pente (orientée vers le bas) de la surface isobare et Onla normale à la surface isobare (orientée vers le haut, c’est-à-dire vers les basses pressions); soit Osun axe constituant avec Onet Otun trièdre de référence O(s , t , n ) trirectangle et direct: l’axe Osest donc tangent à la ligne de niveau de la surface isobare passant par O.

Les deux forces は et て étant situées dans le plan vertical passant par la ligne de plus grande pente Ot 轢, il faut nécessairement, pour que le système des trois forces en jeu soit en équilibre, que la troisième force ぢ soit également située dans

ce plan. Prenons donc ce plan des forces comme plan de figure (fig. 2). Décomposons la force de Coriolis ぢ en ses deux composantes C^h et C^z respectivement sur un axe horizontal Ohet sur un axe vertical Oz 轢; décomposons de même la force de pression は en ses deux composantes P^h et P^z .

Direction du vent

La vitesse ふ du vent synoptique étant horizontale et perpendiculaire à la force de Coriolis ぢ, le vecteur ふ est perpendiculaire en O au plan de la figure 2 et orienté de telle façon que la force de Coriolis soit dirigée sur sa droite dans l’hémisphère Nord.

On peut donc énoncer la loi suivante: le vent synoptique en un point O de l’atmosphère libre est tangent à la ligne de niveau de la surface isobare qui passe en ce point et souffle dans une direction telle qu’il laisse sur sa gauche (dans l’hémisphère Nord) les creux des surfaces isobares.

La ligne de niveau de la surface isobare p qui passe par le point O (intersection de la surface isobare par un plan horizontal) est également l’isobare de cote p dans le plan horizontal en question. Il est donc possible d’énoncer la règle précédente sous une autre forme plus familière (loi de Buys-Ballot): le vent synoptique en un point O est tangent à l’isobare passant par ce point et souffle dans une direction telle qu’il laisse les basses pressions sur sa gauche (dans l’hémisphère Nord).

Le parallélisme du vent et de l’isobare se vérifie parfaitement sur les cartes météorologiques relatives à l’atmosphère libre (cartes à un niveau supérieur à 1 ou 2 kilomètres). Cette vérification est une preuve que le frottement et la viscosité de l’air atmosphérique sont négligeables à l’échelle synoptique en atmosphère libre. Au voisinage du sol, en revanche, le vent fait un certain angle avec l’isobare: le vent au sol est quelque peu convergent vers les centres de basse pression et quelque peu divergent des centres de haute pression. Le fait que le vent en atmosphère libre est parallèle à l’isobare, plutôt que perpendiculaire comme il pourrait sembler logique, est dû à l’intervention de la rotation terrestre. Si la Terre était environnée de nuages masquant les astres, le parallélisme du vent et de l’isobare constituerait une preuve de la rotation de la Terre, au même titre que la célèbre expérience du pendule de Foucault.

Équilibre des forces

L’équilibre des forces se traduit par les deux équations:

– en projection sur l’horizontale Oh :

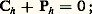– en projection sur la verticale Oz :

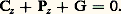En désignant par 見 l’inclinaison de la surface isobare (sa pente est tan 見), on a:

Comme l’angle 見 est toujours petit, la composante P^h est très petite devant P^z .

La force de Coriolis ぢ est elle-même très petite (la vitesse du vent n’atteint jamais celle d’un obus par exemple), de sorte que ses deux composantes C^h et C^z sont très petites.

La composante horizontale C^h de la force de Coriolis équilibre la composante horizontale P^h de la force de pression, tandis que la composante verticale C^z n’intervient que de façon négligeable dans l’équilibre vertical devant l’importance de la force de pesanteur て et de la composante verticale P^z de la force de pression.

L’expression de la composante horizontale C^h est: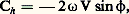

où 諸 est la vitesse de rotation angulaire de la Terre ( 諸 = 2 神/86 164 rad.s^-1), V la vitesse du vent et sin 﨏 le sinus de la latitude du lieu.

D’autre part, puisque:

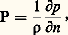on a: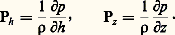

Avec une très bonne approximation, les deux relations d’équilibre précédentes peuvent donc s’écrire:

De la première expression on tire:

relation qui lie la vitesse du vent au gradient horizontal de pression; et de la seconde on déduit: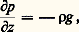

qui traduit le fait que l’atmosphère peut être considérée comme en équilibre hydrostatique.

En projetant les forces en présence sur la ligne de plus grande pente Otde la surface isobare, on élimine la force de pression qui est normale à cette surface.

L’équation d’équilibre sur Ots’écrit:

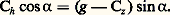En négligeant C^z devant g et C^z sin 見 devant C^h cos 見, ce qui est légitime vu la petitesse de l’angle 見, on obtient:

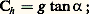d’où, en remplaçant C^h par sa valeur:

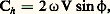on obtient l’expression suivante:

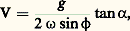relation qui lie la vitesse du vent à la pente de la surface isobare. Dans cette formule, la masse volumique 福 de l’air ne figure pas explicitement (elle figure implicitement dans tan 見).

On notera que la relation précédente n’est pas valable au voisinage de l’équateur, où sin 﨏 devient nul. Dans cette région, c’est l’accélération du vent qui équilibre le gradient de pression, d’ailleurs généralement beaucoup plus faible qu’aux autres latitudes.

5. Vent géostrophique et vent du gradient

Le vent déterminé par l’une des deux formules précédentes en fonction du gradient horizontal de pression ou en fonction de la pente de la surface isobare est souvent désigné sous le nom de vent géostrophique.

L’hypothèse de départ est que l’accélération de l’air est négligeable. Mais l’accélération d’un mobile sur sa trajectoire peut être décomposée en:

– une composante tangentielle dirigée dans le sens de la vitesse ou opposée à cette dernière (cette composante est effectivement négligeable à l’échelle synoptique);

– une composante centrifuge perpendiculaire à la vitesse qui, dans le cas de trajectoires très courbées (écoulement de l’air dans un cyclone par exemple), peut atteindre des valeurs suffisamment importantes pour qu’il n’apparaisse plus légitime de la négliger.

L’expression de cette accélération est V²/R, où V est la vitesse du mobile (vitesse du vent) et R le rayon de courbure de la trajectoire (rayon du cercle osculateur à la trajectoire au point considéré). Cette accélération centrifuge est, selon le sens de la courbure de la trajectoire, dirigée sur la droite ou sur la gauche du vent; elle est donc, selon le cas, de même sens que la composante P^h de la force de pression ou de sens opposé. L’équation du vent devient donc:

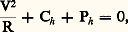le rayon de courbure R étant compté positivement lorsque la force centrifuge s’ajoute à la composante horizontale P^h de la force de pression, c’est-à-dire pour les trajectoires à courbure anticyclonique, et négativement pour les trajectoires à courbure cyclonique. On obtient, avec cette convention, l’équation du vent du gradient:

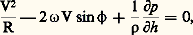équation du second degré qui fournit la vitesse V du vent en tenant compte de la courbure de la trajectoire.

Si l’on désigne par V^gr la vitesse du vent du gradient et par V^g la vitesse du vent géostrophique, l’équation précédente peut s’écrire:

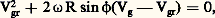puisque la vitesse du vent géostrophique V^g est donnée par la formule:

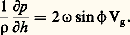On peut encore écrire:

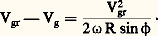Ainsi, dans le cas d’une courbure cyclonique (R 麗 0) de la trajectoire, cette différence est négative; le vent géostrophique correspond à une surestimation par rapport au vent du gradient. Pour une trajectoire à courbure anticyclonique, en revanche (R 礪 0), il y a lieu d’apporter au vent géostrophique une correction positive pour obtenir le vent du gradient.

6. Variation du vent avec l’altitude. Apparition du courant-jet

La formule de l’approximation géostrophique permet de comprendre comment, à un niveau donné, le vent s’organise en fonction de la distribution de la pression à ce niveau. L’étude de la variation de la pression avec l’altitude va permettre d’expliquer les variations du vent avec l’altitude et, en particulier, l’apparition de vents forts au-dessus de certaines régions.

Variation de la pression avec l’altitude

Pour étudier les conditions d’équilibre vertical d’une particule d’air, on peut isoler, par la pensée, une colonne d’air du milieu qui l’entoure en remplaçant ce milieu par l’action qu’il exerce sur cette colonne. Soit ainsi une colonne d’air AB s’étendant depuis la surface du globe jusqu’à la limite de l’atmosphère (fig. 3).

Une particule d’air limitée par deux niveaux H et H de cette colonne est soumise aux forces latérales de pression, qui, opposées, s’annulent; aux forces de pression verticales p et p , qui s’exercent respectivement sur la base et le sommet de la particule; au poids P de la particule, vertical et dirigé vers le bas.

En prenant pour unité de surface la section de la colonne et en écrivant l’équilibre de ces forces, on obtient: p 漣 p = P; la différence de pression p 漣 p entre la base et le sommet d’une colonne d’air de section unité est égale au poids de cette colonne d’air.

On en déduit, d’une part, que la pression diminue toujours avec l’altitude et, d’autre part, que la pression à la base d’une colonne d’air de hauteur infinie est égale au poids total de cette colonne d’air. L’air froid étant plus dense que l’air chaud, il en résulte immédiatement que la pression décroît plus rapidement avec l’altitude dans l’air froid que dans l’air chaud. Autrement dit, l’épaisseur d’une couche d’air contenue entre deux surfaces isobares déterminées p et p est plus grande dans l’air chaud que dans l’air froid.

On comprend alors facilement comment varie la pente des surfaces isobares avec l’altitude, compte tenu de la répartition horizontale des températures.

Considérons en effet deux surfaces isobares superposées de cotes p et p . On voit, sur la figure 4 a, que, si l’air est relativement plus froid du côté des basses pressions (ou des creux des surfaces isobares), la pente de la surface isobare supérieure p est plus grande que la pente de la surface inférieure p . Dans le cas contraire (fig. 4 b), la pente de la surface isobare supérieure p est plus faible que la pente de la surface isobare inférieure p .

Le vent thermique

Compte tenu de la relation entre vent et pente des surfaces isobares, le vent croît avec l’altitude lorsque la température décroît des hautes vers les basses pressions (des sommets des surfaces isobares vers les creux), et inversement.

Le vent croît avec l’altitude lorsque le gradient horizontal de température est dirigé selon le gradient horizontal de pression.

Si l’on se place dans des conditions telles que le vent croisse avec l’altitude à partir du sol, on en conclut que la vitesse du vent augmente jusqu’au niveau où le gradient horizontal de température s’annule pour, ensuite, s’inverser. Ce niveau est donc celui de l’axe du courant-jet (maximum du vent). Cela s’exprime simplement sous une forme mathématique. En effet, en dérivant l’équation du vent géostrophique par rapport à la pression (prise comme variable d’altitude), on obtient l’expression: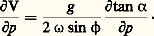

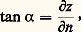
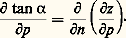Si z est l’altitude de la surface isobare de cote p , on a:

n étant compté selon la ligne de plus grande pente (du bas vers le haut), et:

L’équation de base de l’équilibre hydrostatique:

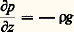permet d’écrire:

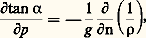où 福 est la masse volumique de l’air au niveau z considéré. On a donc:

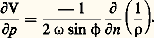En tenant compte de l’équation des gaz parfaits: p = RT 福, valable pour l’air et pour une pression p constante (surface isobare), on a donc:

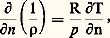où T est la température de l’air au niveau z et R la constante des gaz parfaits, d’où:

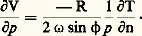Si 煉T 煉n 礪 0, la température croît des basses pressions (creux des surfaces isobares) vers les hautes pressions (sommet des surfaces isobares), c’est-à-dire des hautes pressions chaudes vers les basses pressions froides, 煉V 煉p est négatif: le vent croît quand p décroît, c’est-à-dire que le vent croît avec l’altitude. Dans ce cas, le maximum de vent se situe au niveau où 煉T 煉n s’annule pour devenir négatif.

Si 煉T 煉n 麗 0, les régions où la pression est basse par rapport à celles où la pression est haute sont relativement chaudes, 煉V 煉p est positif: le vent décroît avec l’altitude (c’est-à-dire quand p décroît). Dans ce cas, le niveau où 煉T 煉n s’annule pour devenir positif correspond au minimum de la vitesse du vent. En raison de cette relation les météorologistes parlent de vent thermique pour désigner la variation du vent avec l’altitude. Le vent thermique est souvent un vent d’ouest puisque la température décroît lorsque la latitude augmente, au moins du tropique vers le pôle. Il se renforce au-dessus des façades orientales des continents où le contraste thermique s’accentue. Au-dessus de l’Afrique, en été, l’air saharien surchauffé est au nord de l’air océanique de la mousson, plus humide et plus frais: le vent thermique est alors un vent d’est.

7. Climatologie des courants-jets

Courants-jets et fronts

L’analyse qui précède ayant révélé que la variation du vent selon la verticale était liée au gradient horizontal (ou, plus précisément, au gradient isobare) de température, il est logique de s’attendre à trouver les vents forts au-dessus des régions du globe où la température varie rapidement dans le sens horizontal (ou, plus précisément, le long des surfaces isobares, presque horizontales) et lorsque cette forte variation de température s’observe au sein d’une couche d’air très épaisse.

Ces deux conditions se trouvent réunies, en particulier, de façon régulière au voisinage du front polaire qui sépare, dans toute l’épaisseur de la troposphère, les masses d’air polaires des masses d’air tropicales. On vérifie, en effet, la présence du courant-jet le long du front polaire.

Cette conclusion est importante: elle permet notamment d’identifier la climatologie du courant-jet à celle du front polaire. Elle conduit à refuser l’image d’un courant-jet continu ceinturant le globe (dans l’hémisphère Nord et dans l’hémisphère Sud), car la «cloison» que constitue le front polaire, loin d’être continue, comporte des interruptions correspondant aux «décharges» d’air polaire qui se déversent des hautes latitudes jusqu’aux latitudes tropicales.

Bien entendu, les seuls fronts polaires n’ont pas l’apanage d’être accompagnés d’un courant-jet, et le phénomène peut apparaître en liaison avec tout front bien marqué, c’est-à-dire lié à un fort gradient horizontal de température et intéressant une part importante de la troposphère; mais les fronts polaires sont généralement mieux marqués que les fronts arctiques ou intertropicaux.

La partie gauche de la figure 5 représente la coupe verticale théorique d’un front. Les dimensions verticales de la coupe sont fortement dilatées par rapport à la distance horizontale. Le diagramme de la partie droite de la figure 5 comporte, en abscisses, la température de l’air et, en ordonnées, l’altitude, cette dernière étant commune aux deux parties, gauche et droite, de la figure. On a schématisé à droite les résultats de deux sondages de température effectués de part et d’autre du front, c’est-à-dire l’un dans l’air polaire et l’autre dans l’air tropical. On voit immédiatement que, si l’air polaire est plus froid que l’air tropical dans la basse troposphère, c’est l’inverse qui se produit dans la stratosphère, le gradient horizontal de température s’annulant à un niveau intermédiaire entre celui de la tropopause polaire et celui de la tropopause tropicale. D’après ce que nous avons dit antérieurement, c’est ce niveau qui marque le maximum de vent . On a tracé, sur la partie gauche de la figure, les isolignes de la vitesse du vent.

La figure 6, établie pour un cas réel, permet bien de retrouver les grandes lignes du schéma de la figure 5, et cet accord satisfaisant justifie l’approche théorique élémentaire du phénomène. La figure 7 est une image dans l’infrarouge prise par le satellite Météosat le 16 septembre 1983. L’étirement des nuages supérieurs, qui apparaissent en blanc d’autant plus intense qu’ils sont plus élevés, met en évidence un courant-jet sur l’Atlantique nord et l’Europe. Il se situe sur la face ouest d’une bande perturbée, à l’est de Terre Neuve, et se prolonge sur le golfe de Gascogne et le sud de la France.

Courants-jets et navigation aérienne

Les tubes des courants-jets, qui s’étendent parfois sur des distances de plusieurs milliers de kilomètres et dont la vitesse dépasse fréquemment 300 kilomètres par heure, présentent, pour la navigation aérienne, un puissant intérêt, soit qu’elle les recherche lorsqu’ils sont favorables à l’amélioration des temps de vol, soit qu’elle les fuie lorsqu’ils s’opposent à la marche de l’avion. L’établissement des plans de vol tient compte de leur localisation observée et prévue, ce qui permet de réaliser de précieuses économies de carburant. De plus, les forts gradients de la vitesse du vent observés sur le pourtour des tubes des courants-jets et, notamment, sur leur face «froide» (tournée vers le pôle), sont favorables au déclenchement de mouvements tourbillonnaires qui se traduisent sur un avion en vol par une turbulence accusée pouvant être suffisamment puissante pour mettre en péril la structure de l’appareil.

Encyclopédie Universelle. 2012.